Chapter 6 - Unbound States

Reference Quantum Mechanics: A Paradigms Approach by David McIntyre.

In bound states, the energy levels of particles are quantized - they are restricted to specific values. In unbound states, energy is no longer quantized, and operates on a continuum.

We still, however, will use the energy eigenvalue equation, its associated Hamiltonian, and the energy eigenvalue wave differential equation. $$\hat{H}|E⟩=E|E⟩$$ $$\hat{H}=\frac{{\hat{p}}^2}{2m}+V(\hat{x})$$ $$\left(-\frac{{\hslash }^2}{2m}\frac{d^2}{d{x}^2}+V(x)\right){\psi }_E(x)=E{\psi }_E(x)$$

Free particle eigenstates

For a free particle, $V(x)$ is zero everywhere, so the EEV differential equation becomes $$\frac{d^2}{d{x}^2}{\psi }_E(x)=-k^2{\psi }_E(x)$$ where $k^2=\frac{2mE}{{\hslash }^2}$. This has the general solution of $${\psi }_E(x)=A{e}^{ikx}+B{e}^{-ikx}$$ Since we're no longer in a bound state, we no longer have constraints on extrema (except for the normalization condition) - and hence continuous energy, no longer quantized. We can apply the Schrödinger time evolution to this by multiplying the energy basis (above) by a phase factor, such that $$\begin{array}{rl}{\psi }_E(x,t)& ={\psi }_E(x)e^{-iEt/\hslash }\\ & =A{e}^{ikx}+B{e}^{-ikx}\end{array}$$ Using the Planck energy relation $E=hf=\hslash \omega$, $${\psi }_E(x,t)=A{e}^{i(kx-\omega t)}+B{e}^{-i(kx+\omega t)}$$ This wave function represents a wave that retains its shape as it moves, with a speed determined by $|v|=\omega /k$, the phase velocity.

Thus, $A{e}^{i(kx-\omega t)}$ represents the part moving in the positive direction, while $B{e}^{-i(kx+\omega t)}$ represents the part moving in the negative direction.

We can also use $${\psi }_k(x)=A{e}^{ikx}$$ to represent the wave vector eigenstates, with the sign of $ikx$ indicating the direction of motion.

Note: we need both positive and negative $k$ values to make a general energy eigenstate.

Momentum Eigenstates & de Broglie Relation

The momentum eigenvalue equation is $$\hat{p}{\psi }_p(x)=p{\psi }_p(x)$$

This is equivalently $\hat{p}|p⟩=p|p⟩$ in braket notation.

Applying $\hat{p}$ to ${\psi }_k(x)$ above, $$\hat{p}{\psi }_k(x)=\left(-i\hslash \frac{d}{dx}\right)A{e}^{ikx}=\hslash k{\psi }_k(x)$$ implying that $p=\hslash k$ is the momentum eigenvalue with an associated eigenstate $${\psi }_p(x)=A{e}^{ipx/\hslash }$$

Note: this is a function of position $x$, not momentum $p$: $x$ is the independent variable while $p$ is the particular momentum eigenvalue.

Since $k=2\pi /\lambda$, we can use our momentum eigenvalue $p$ to create the de Broglie relation: $${\lambda }_{\text{de Broglie}}=\frac{h}{p}$$ The momentum eigenstates are also energy eigenstates for our free particle, with energy $$E=\frac{p^2}{2m}$$

This means that the momentum and energy operators commute. Any given momentum eigenstate will have some energy given by the above equation, but some energy state doesn't necessarily have a definite momentum, since a single energy state usually corresponds to 2+ momentum states - meaning the energy state is degenerate.

Momentum W.E.

The time-dependent wave equation governing a momentum eigenstate is $${\psi }_p(x,t)={\psi }_p(x)e^{-i{E}_{p}t/\hslash }=A{e}^{ip/\hslash (x-pt/2m)}$$ with a probability density given by 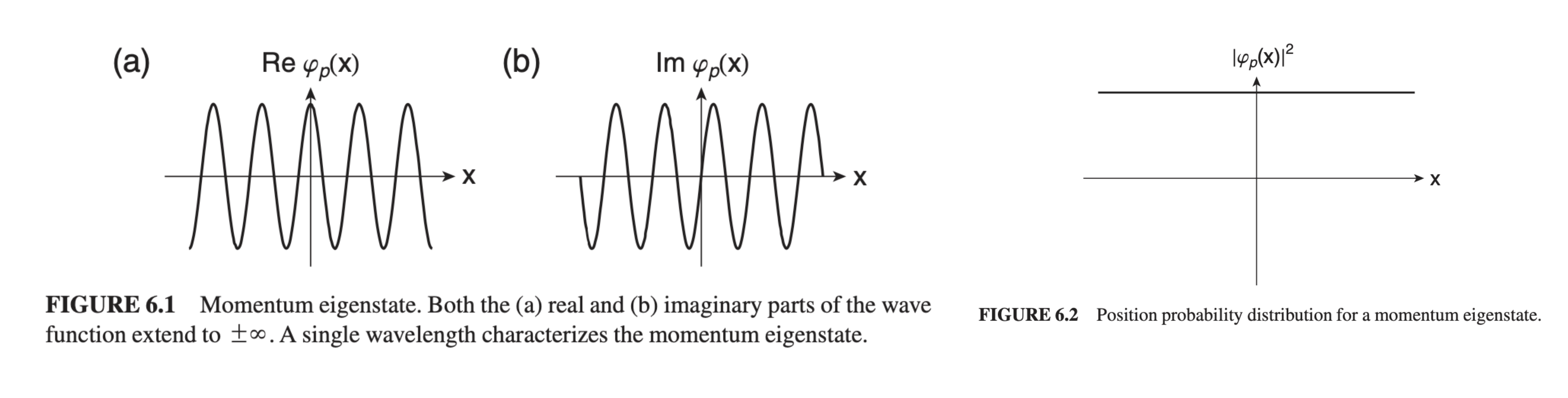$$\mathcal{P}(x)=|{\psi }_p(x){|}^2=|A{|}^2$$ Unfortunately, this momentum eigenstate is constant regardless of position - it is spread out over all space unto $\infty$. This makes the momentum eigenstate impossible to normalize - unless we create a superposition of momentum eigenstates to create wave packets.

Review on Basis States:

All basis state should demonstrate

$$\begin{array}{rl}⟨a_i|a_{j\ne i}⟩=0& \text{orthogonality}\\ ⟨a_i|a_i⟩=1& \text{normalization}\\ \sum _i|a_i⟩⟨a_i|=\vec{1}& \text{completeness}\end{array}$$ with the orthogonality and normalization conditions able to be written in the form of the Kronecker delta: $$⟨a_i|a_j⟩=\delta ij=\{\begin{array}{ll}0& \text{if}i\ne j,\\ 1& \text{if}i=j\end{array}$$ The Dirac delta function is the Kronecker delta used for continuous, rather than discrete sets, where $$\delta (x-x_0)$$ is a function that is zero for all $x$, except at $x=x_0$, where it is infinite.

Thus, the orthonormality condition for the momentum eigenstate can be expressed in Dirac notation like this: $$⟨p^{\prime \prime }|p^{\prime }⟩=\delta (p^{\prime \prime }-p^{\prime })$$ which can be translated into wave function notation using the rules from Chapter 5: $${\int }_{-\infty }^{\infty }{\psi }_{p^{\prime \prime }}^{\ast }(x){\psi }_{p^{\prime }}(x)dx=\delta (p^{\prime \prime }-p^{\prime })$$ If we define our normalization constant $$A=\frac{1}{\sqrt{2\pi \hslash }}$$ then our normalized momentum eigenstates are $${\psi }_p(x)=\frac{1}{\sqrt{2\pi \hslash }}{e}^{ipx/\hslash }$$

Momentum P.D.

If we wanted to find the probability amplitude for some general state $|\psi ⟩$ to have momentum $p$ (i.e the projection of the general state $|\psi ⟩$ onto momentum basis $|p⟩$), we'd want to find $$⟨p|\psi ⟩=\psi (p)$$ ... however, we're using $p$ in place of $x$ in our wave-function.

... but wait! $\psi (x)$ and $\psi (p)$ are not the same functions. They're the general state operating in different bases.

So ... let's just represent this momentum wave function with a different symbol instead. $$\varphi (p)=⟨p|\psi ⟩$$ This is known as the momentum space wave function, a continuous wave function that represents the quantum state vector in terms of the momentum eigenstates.

The sinusoidal waves that make up this momentum eigenstate can be combined using the Fourier transform of $\varphi (p)$ to form a combined "wave packet" with a location in the $x$ basis, given by $$\psi (x)=\frac{1}{\sqrt{2\pi \hslash }}{\int }_{-\infty }^{\infty }\varphi (p)e^{ipx/\hslash }dp$$ ... which we can also write in the $p$ basis with an inverse Fourier transform: $$\varphi (p)=\frac{1}{\sqrt{2\pi \hslash }}{\int }_{-\infty }^{\infty }\psi (x)e^{-ipx/\hslash }dx$$

Wave Packets

Wave packets are localized superpositions of smaller waves that obey constructive and destructive interference.

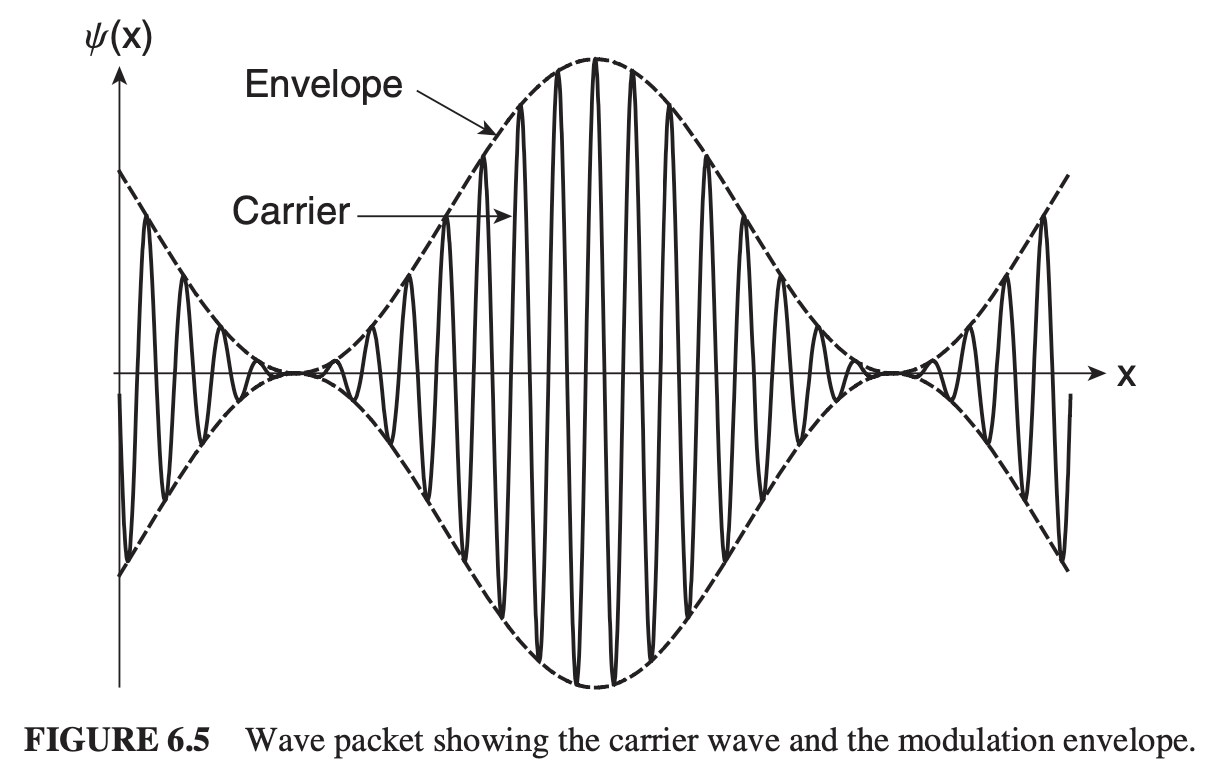The wave packet envelope and carrier often move at different speeds. There is much more to this chapter, but I think I'll call it here for now and write up a study guide for the imminent final.