Chapter 6 - Magnetic Fields in Matter
Reference "Introduction to Electrodynamics" (5e) by David Griffiths.
If a material is placed in a -field, it will acquire a magnetic polarization (or magnetization). Different materials acquire different polarizations depending on their atomic structures.
- Paramagnets: magnetization parallel to applied , materials with odd # of electrons.
- Diamagnets: magnetization antiparallel to applied , materials with an even # of electrons.
- Ferromagnets: magnetization persists on the material even after the applied -field is removed, and is determined by the whole "magnetic history" of the object.
All electrons act as magnetic dipoles.
Imagine a magnetic dipole as pointing from south to north (the Gilbert model). It's an inaccurate model at small scales according to Griffiths, but he recommends it for intuition.
Torques and Forces on Magnetic Dipoles
Magnetic dipoles will experience some torque in an applied field, where and is the magnetic dipole moment, defined (for current loops) as where is the "vector area" of the loop, which is just the enclosed area if the loop is flat. The direction of follows the right-hand rule.
In a uniform field the net force on the dipole is zero, though this is not the case for nonuniform fields.
For an infinitesimal loop with dipole moment in field , the force on the loop is
Diamagnets
Diamagnetism affects all materials, but is much weaker than paramagnetism, so is most easily observed in materials with an even number of electrons.
When an external -field is applied to a material, individual electrons will speed up according to where is the "radius" of the electron from the nucleus of an atom. This increase in orbital speed will change the dipole moment this change in the dipole moment is antiparallel to as shown above.
Magnetization
Magnetization is For a paramagnet, perhaps suspended above a solenoid, the magnetization would be positive/upward, and force downward. For a diamagnet, the magnetization would be instead downward, and force upward.
In general in a nonuniform field, paramagnets are attracted into the field, and diamagnets are repelled away.
Note: is an average over a wildly complex set of infinitesimal dipoles and "smooths out" the dipole into a macroscopic view.
Note: both diamagnetism and paramagnetism are quite weak compared to, for instance, ferromagnetism, and so are often neglected in experimental calculations.
Field of a Magnetized Object
For some single dipole, the magnetic vector potential is For a magnetized object with magnetization , Alternatively, we can look at the object in terms of its volume current density and surface current density , where
This means the potential (and therefore magnetic field) is the same as would be made by some volume current throughout the material plus the surface current on the boundary.
This means we needn't integrate all the infinitesimal dipoles, but rather just determine the bound currents and and find the field they produce.
Note:
Auxiliary Field
The auxiliary field is, in a sense, the magnetic field since, it represents the real-world field we'd observe - including both the magnetic flux field and magnetism .
The free current is the current composed of moving free electrons (often caused by a battery or other current).
The bound current results from the magnetic polarization (magnetization) of individual electrons into dipoles - Griffiths represents each dipole as tiny current loops. Individually, the current loop of each individual atom tend to cancel one another out, except at the boundary where there are no adjacent atoms - thus the bound current density represents a current around the boundary of the surface (see this image).
"It is a peculiar kind of current, in the sense that no single charge makes the whole trip - on the contrary, each charge moves only in a tiny loop within a single atom. Nevertheless, the net effect is a macroscopic current flowing over the surface of the magnetized object." - Griffiths
The total current density is then the free-charge-current density plus the magnetized current density (or bound current). Ampère's law can be then written as
We can simplify by moving both curls to the left
This curl grouping is called the auxiliary field .
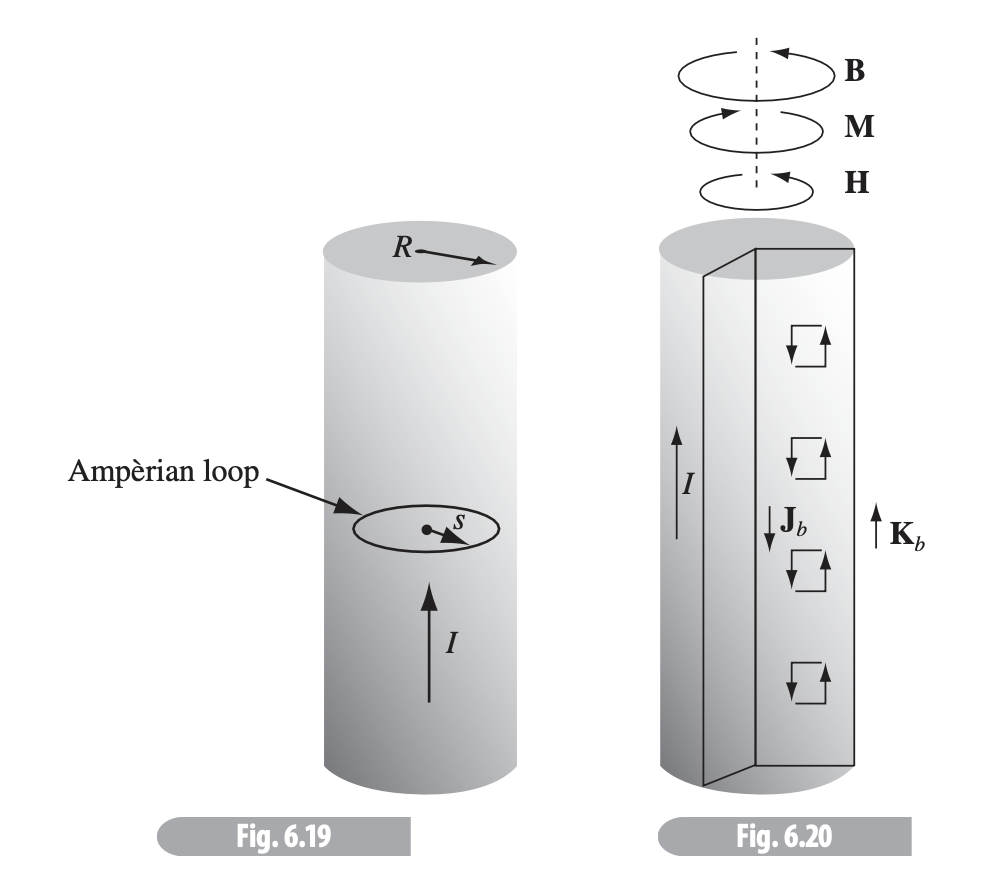 Ampère's law becomes
where is the free current passing through the Ampèrian loop.
Ampère's law becomes
where is the free current passing through the Ampèrian loop.
We see when looking at a magnetometer. is difficult to isolate unless we know both the exact amount of current and/or the magnetic properties of the material, such that we can evaluate .
Note / warning:
, though more physically relevant in some ways, is harder to calculate:
- It has a non-zero divergence
- It cannot be calculated without knowing the material type
Symmetries
If you know the material type, this can be more helpful than the corresponding boundary conditions
Linear & Nonlinear Media
Linear media are those for which is linearly proportional to the magnetic field, .
This is the case for most materials, which tend to be either paramagnetic (odd # of electrons) or diamagnetic (even # of electrons), and the proportionality is (chi) is the magnetic susceptibility of a substance, and is:
- Positive for paramagnets.
- Negative for diamagnets.
- Dimensionless.
- Typically around .

Therefore Thus, , and where is the permeability of a material.
(the permeability of free space) is the case when .
is dimensionless.
To calculate in terms of and :
Ferromagnetism (nonlinear)
Ferromagnets require no external fields to sustain the magnetization, with each magnetic dipole pointing in the same direction as its neighbors.
However - this "pointing" only occurs in small patches called domains, with each domain cancelling the others out (usually), so not all iron devices are fully magnetic.

However, each domain will expand when placed in a sufficiently powerful magnetic field.

From Wikipedia: "Moving domain walls in a grain of silicon steel caused by an increasing external magnetic field in the 'downward' direction, observed in a Kerr microscope. White areas are domains with magnetization directed up, dark areas are domains with magnetization directed down."
If the field is strong enough such that one domain dominates, the iron becomes saturated. However, too-large domains are inherently unstable and will collapse into smaller fields without the presence of a large field, though the similar polarity will be present in each domain, so the iron remains magnetized until other fields affect it to go back to individual domains.
Ferromagnet design
Wrap a coil of wire around the iron to be magnetized, then run a current through it to generate a field. As increases, the domain boundaries move until they reach the saturation point.
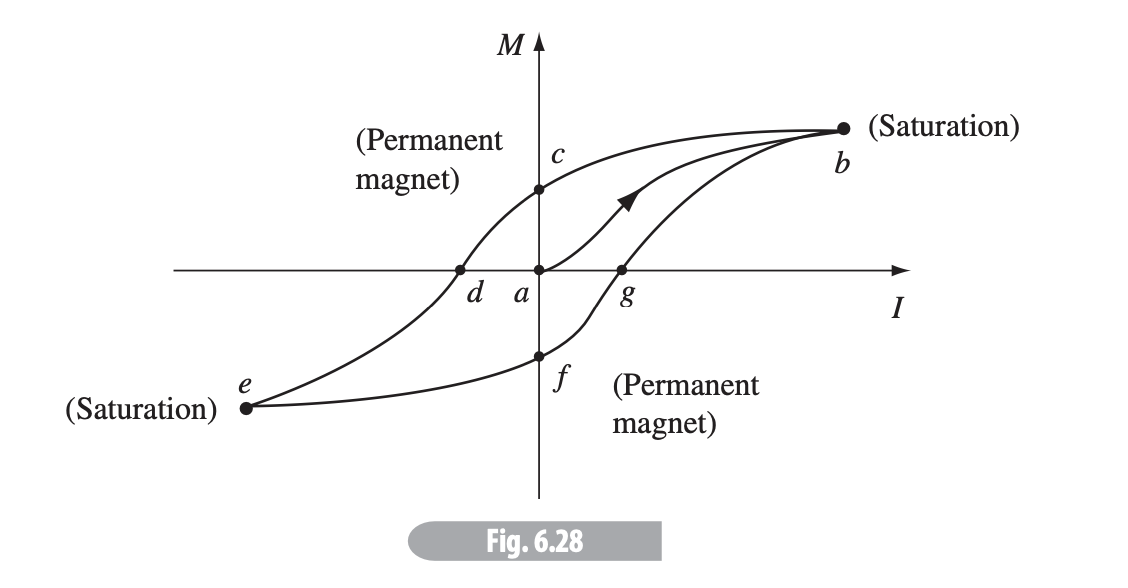 If we turn off the current, the permanent magnet remains. If we, however, run through the coil, we reverse the effect, as shown above, known as a hysteresis loop.
If we turn off the current, the permanent magnet remains. If we, however, run through the coil, we reverse the effect, as shown above, known as a hysteresis loop.
Ferromagnetic "history" may also be reset by increasing the temperature of the iron to 770 C, the Curie point - above this, iron also behaves more like a paramagnet.