Chapter 7 - Electrodynamics

Reference "Introduction to Electrodynamics" (5e) by David Griffiths.

Electrostatics is the study of the electric field $\vec{E}$ of static electric charges; magnetostatics is the study of the magnetic field $\vec{B}$ of moving electric charges. Electrodynamics is therefore the study of the electric field $\vec{E}$ of moving electric charges.

Ohm's Law

To make a current flow, some force on the charges is needed - thus, current density can be written as proportional to the force per unit charge $\vec{f}$. $$\vec{J}=\sigma \vec{f}=\sigma (\vec{E}+\vec{v}\times \vec{B})$$ Usually, the charge velocity is small enough that $\vec{v}\times \vec{B}=0$, so $$\vec{J}=\sigma \vec{E}$$

This is a more primitive variety of Ohm's law, $I=V/R$. Note that $I=\int \vec{J}\cdot d\vec{a}$.

$\sigma$ is the conductivity of a material, with the resistivity being $$\rho =\frac{1}{\sigma }$$

• Metals can be regarded as perfect conductors: $\sigma \approx \infty$
• Insulators/dielectrics: $\sigma \approx 0$

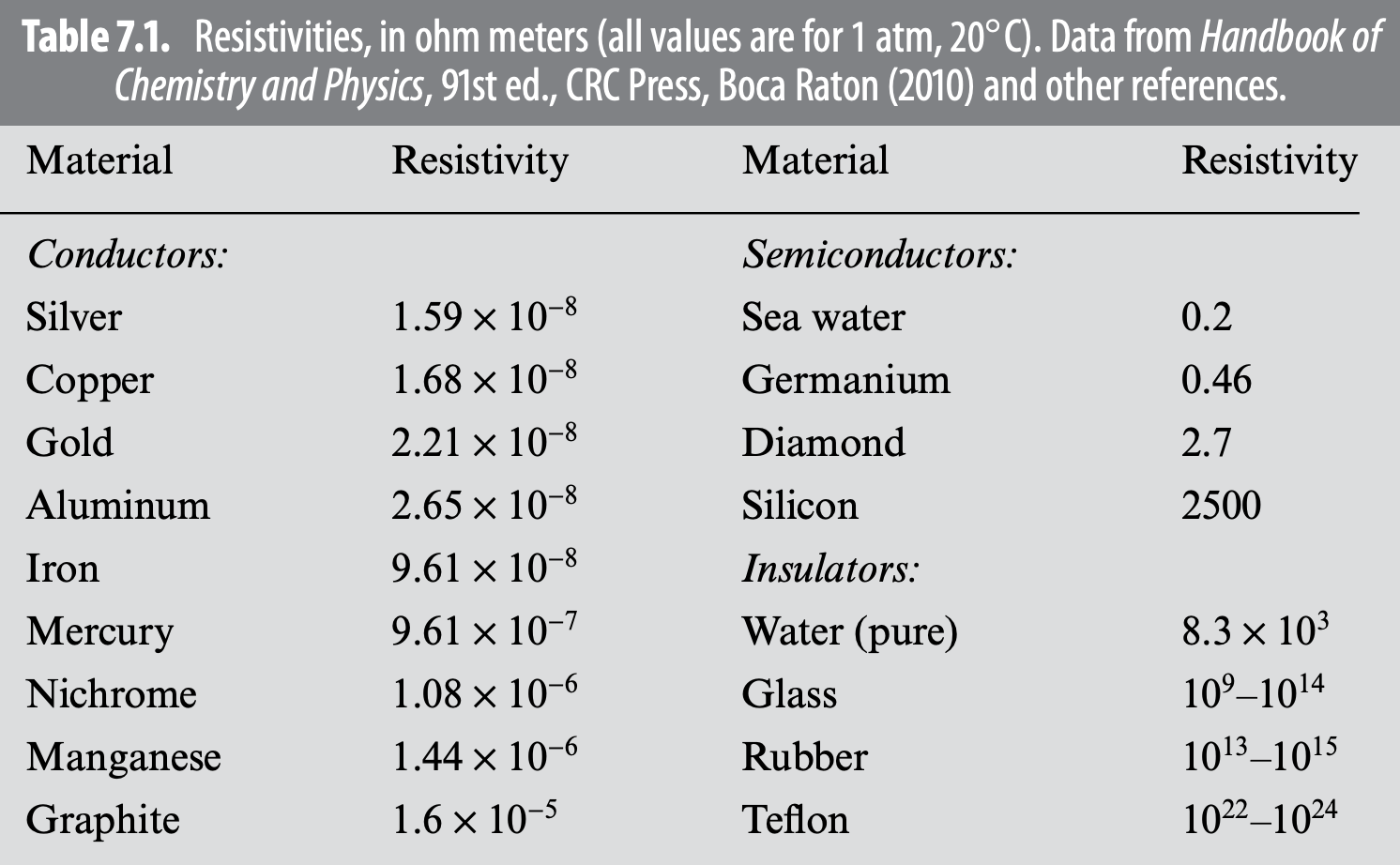
Resistors are made of low-conducting (hence high-resistivity) materials.

Actual resistance $R$ will depend on the dimensions of the material in question: $$R=\frac{\rho L}{A}$$

• $\rho$ is a quality of the material itself, while $R$ depends on the amount of that material used.

Power

Also known as the Joule heating law, power is measured in joules per second and is the amount of "energy" consumed by something, and is defined as $$P=VI=I^{2}R$$

Electromotive Force

Now, regarding the EMF. Electromotive force (or electromotance) is not a force. Rather, it is the integral over the force per unit charge, or the forces driving each electron in a material, and is defined as $$ϵ=\oint \vec{f}\cdot d\vec{l}$$ $\vec{f}=\overrightarrow{f_s}+\vec{E}$, where $\overrightarrow{f_s}$ is the 'source' or 'driving' force on each charge, usually a battery or something to create some potential difference $V$, while $\vec{E}$ "smooths out" the conductor such that we have an equal distribution of electrons everywhere (no buildups).

For an electrostatic circuit, $$\oint \vec{E}\cdot d\vec{l}=0$$ and as such $$ϵ=\oint {\vec{f}}_s\cdot d\vec{l}$$ An ideal EMF source (resistanceless battery) has $\sigma =\infty$, so $\vec{E}=-\overrightarrow{f_s}$ and thus $$V=-{\int }_a^b\vec{E}\cdot d\vec{l}={\int }_a^b{\vec{f}}_s\cdot d\vec{l}\equiv \oint {\vec{f}}_s\cdot d\vec{l}=ϵ$$

$V=ϵ$ for an ideal EMF source (ideal battery).

$ϵ$ is effectively the "work done per unit charge".

Motional EMF

When we move a wire through a magnetic field, we get a motional EMF.

From the Lorentz force law of a single charge moving through a magnetic field, $${\vec{f}}_{\text{mag}}=q(\vec{v}\times \vec{B})$$ EMF is force per unit charge $\vec{f}/q$, so $$\begin{array}{rl}ϵ& =\oint {\vec{f}}_{\text{mag}}\cdot d\vec{l}\\ & =\oint (\vec{v}\times \vec{B})\cdot d\vec{l}\end{array}$$ This is fine, but can get complicated to calculate (as evidenced by homework 6). A much simpler way to calculate $ϵ$ of some loop is via Faraday's law, where $$ϵ=-\frac{d\Phi }{dt}$$ Here, $\Phi$ is the magnetic flux, so $d\Phi /dt$ is the change in magnetic flux through a loop.

EMF only happens when a loop and magnetic field are moving with respect to one another - i.e. if a loop moves further away from a source of magnetic field, or we move our line of current away from our loop.

$$\begin{array}{rl}\Phi & =\int \vec{B}\cdot d\vec{a}\end{array}$$

Flux is really just the amount of magnetic field passing through some loop.

Induction & Faraday's Law

Michael Faraday noted some key things about induction - mainly:

A changing magnetic field induces an electric field.

This is represented by Faraday's law: $$\oint \vec{E}\cdot d\vec{l}=-\int \frac{\partial \vec{B}}{\partial t}\cdot d\vec{a}$$ In differential form, $$\vec{\nabla }\times \vec{E}=-\frac{\partial \vec{B}}{\partial t}$$ Thus, whenever the magnetic flux through a loop changes (or magnetic field $\vec{B}$ changes w.r.t. a loop), an emf of $$ϵ=-\frac{d\varphi }{dt}$$ will appear in the loop.

This emf is often called Faraday's Law of Induction - Griffiths disagrees but Griffiths is Griffiths.

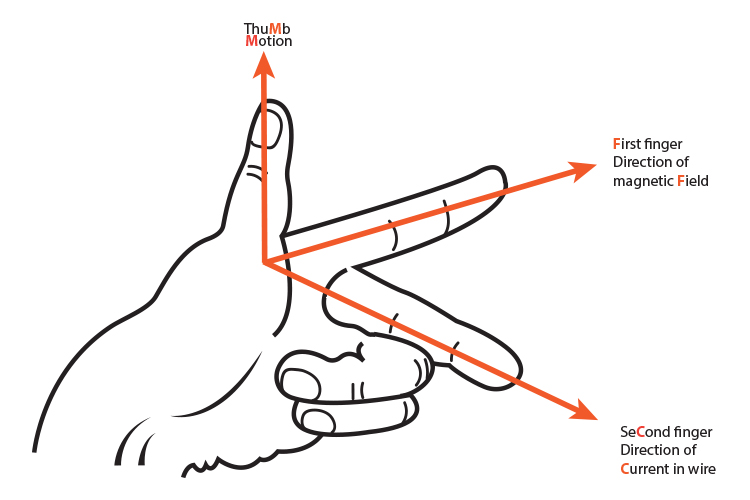
Lenz's Law

In Griffiths' words,

Nature abhors a change in flux.

According to the Wikipedia definition on the subject, "[the] magnetic field created by the induced current opposes changes in the initial magnetic field."

Fleming's right hand rule is a good mnemonic to remember this:

Induced Electric Field

Induced electric fields can be calculated in a manner similar to Ampere's law:

$$\oint \vec{E}\cdot d\vec{l}=-\frac{d\varphi }{dt}$$

The rate of change of magnetic flux plays the same role as ${\mu }_0{I}_{\text{enc}}$.

Mutual Inductance

Say we have two loops with the same current flowing through each.

Let $${\Phi }_2=\int {\vec{B}}_1\cdot d{\vec{a}}_2{\Phi }_1=\int {\vec{B}}_2\cdot d{\vec{a}}_1$$ Since both $B_1$ and $B_2$ are proportional to $I_1$ and $I_2$ respectively, we can rewrite this as $${\Phi }_2=M_{21}{I}_1{\Phi }_1=M_{12}{I}_2$$ If $I_1=I_2$ as shown above, then $${\Phi }_2\equiv M_{21}I{\Phi }_1\equiv M_{12}I$$

With the same currents, the magnetic flux through loop 2 (${\Phi }_2$) must be equal to the flux through loop 1 (${\Phi }_1$), and $$M_{21}=M_{12}$$

Since $ϵ=-\frac{d\Phi }{dt}$, with the same current $I$ and $${ϵ}_2=-\frac{d{\Phi }_2}{dt}=-M\frac{d{I}_1}{dt}$$

Inductors

For several loops with constant current $I$ and mutual inductance $M=L$, $$\Phi =LI$$ with $$ϵ=-L\frac{dI}{dt}$$

Energy in Inductors

$$\frac{dW}{dt}=-ϵI=LI\frac{dI}{dt}$$ If we start with $I=0$ and build it up to $I=I$, the total work done is $$\begin{array}{rl}W& =\frac{1}{2}L{I}^2\\ & =\frac{1}{2{\mu }_0}\int B^{2}d\tau \end{array}$$

Maxwell's Equations

Prior to Maxwell, we had four equations governing electric and magnetic fields: $$\begin{array}{rl}\vec{\nabla }\cdot \vec{E}& =\frac{1}{{ϵ}_0}\rho \text{Gauss’s law}\\ \vec{\nabla }\cdot \vec{B}& =0\\ \vec{\nabla }\times \vec{E}& =-\frac{\partial \vec{B}}{\partial t}\text{Faraday’s law}\\ \vec{\nabla }\times \vec{B}& ={\mu }_0\vec{J}\text{Ampeˋre’s law}\end{array}$$

However, these equations fail to account for two things:

• Ampère's law stops applying for nonsteady currents.
• $\nabla \cdot (\nabla \times \vec{B})=0$, but ${\mu }_0(\nabla \cdot \vec{J})=-\frac{\partial \rho }{\partial t}$ (generally).

The key issue here is thus:

Changing electric fields induce magnetic fields, just as changing magnetic fields induces an electric field.

Maxwell added a "displacement current" term ${\vec{J}}_d$ to "fix" Ampère's law: $${\vec{J}}_d={ϵ}_0\frac{\partial \vec{E}}{\partial t}$$ such that, now $$\vec{\nabla }\times \vec{B}={\mu }_0\left(\vec{J}+{\vec{J}}_d\right)$$

This term is only visible in the presence of changing electric fields - magnetodynamics.

In terms of our "usual" form of Ampère's law, $$\oint \vec{B}\cdot d\vec{l}={\mu }_0{I}_{\text{enc}}+{\mu }_0{ϵ}_0\int \frac{\partial \vec{E}}{\partial t}\cdot d\vec{a}$$

The Equations

$$\begin{array}{rl}\vec{\nabla }\cdot \vec{E}& =\frac{1}{{ϵ}_0}\rho \\ \vec{\nabla }\cdot \vec{B}& =0\\ \vec{\nabla }\times \vec{E}& =-\frac{\partial \vec{B}}{\partial t}\\ \vec{\nabla }\times \vec{B}& ={\mu }_0\vec{J}+{\mu }_0{ϵ}_0\frac{\partial \vec{E}}{\partial t}\end{array}$$